數控係統的一個發（fā）展方向, 而五軸聯動數控機床是複雜曲麵高效加工的最佳手段. 在常規CAM 係統輸出的五軸加工程序中, 複雜曲（qǔ）麵加工的刀具路徑是（shì）用小直線和圓（yuán）弧近似逼近的, 這種（zhǒng）近似會產生兩（liǎng）個問題: ¹ 為了達（dá）到加工精度的要求, CAM 係統需要生成更加密集的小直線和圓弧擬合的曲線段, 同時相應表達的N C 代碼也變得更多, 而且隨著加工精（jīng）度要求的（de）提高, NC 代碼（mǎ）量會成倍（bèi）增加. 這樣的處理方式不僅（jǐn）加重了CAD/ CAM 係統和CNC 係統的傳輸負擔, 同時也占用了過（guò）多的CN C 存儲空間（jiān）. 因此, 考慮到加工時間和加工耗費, 常（cháng）規插補方式效率低而且不經濟（jì）. º 由於曲線是由小線段和圓弧擬合而成, 會導致曲（qǔ）線在節點處的速度（dù）和加速度的不連續（xù）, 這樣會導致加工過（guò）程中的（de）進給率波動過大, 降低加工精度和表麵質量.

    為解決以（yǐ）上（shàng）問題, 國內外一些學者提出采（cǎi）用參（cān）數化插補的方法代替常規線性插補. 在這種參數曲線插補中, 非均勻有理B 樣條( NU RBS ) 是（shì）在（zài）參數化插補中得到最廣泛應用的一種曲線表達方（fāng）式. 在幾何描述上（shàng）, N URBS 曲線能用（yòng）比小線段和圓弧更（gèng）少的數據來描（miáo）述曲線, 因此（cǐ）能減少數據量, 減少CAD/ CAM 和CNC 之間的傳輸時間; NURBS 曲線的C2 參數連續保證在插補過程中進給速度和加速度的平滑. 正是基於NU RBS 曲線表達（dá）的這（zhè）些優勢,越來越多的商用CAD/ CAM 係統及內核ACIS 與Paraso lid 都（dōu）先後開發擴充了NURBS 功能.

     現有的高檔數控（kòng）係統, 例如FA NUC、MITSUBISHI 等, 也開發（fā）出了五軸N URBS 插補功能模（mó）塊（kuài）. 文（wén）獻[ 1-3] 中也提出了NURBS 插補算法（fǎ）. 在該算法中, CAM 係統及後處理程序完成刀位點的坐標變換和五軸進給命令輸（shū）出; 其NU RBS 功能（néng）是CAM 係統直接輸出在機床坐標（biāo）係下由兩條多項式曲線定義各軸移動指令（lìng）, 其中: 一條三維的參數曲線定義3 個平動軸x、y、z的運動; 一條二維（wéi）的參數曲線定義轉動軸A 、B、C 的運動（dòng）, 2 條參數曲線采用相同的控製節點序（xù）列. 然而這種方法輸入的僅僅是機床坐標係下的移動指令, 限製了插補模塊的功能, 加工的誤差和速度控製缺乏一定的擴（kuò）展性. 問題主要表現在:

     ( 1) 五軸加工需要進行坐標轉換, 而在坐標轉換的過程中會存在較大的非線性誤差, 而（ér）非線（xiàn）性誤差（chà）的控製是五軸高速高精度加工的關鍵問題[ 4, 5] . ( 2) 該（gāi）方法移動指令所表示的是（shì）刀位（wèi）信息, 無法得到準確的刀尖點的信息, 因此, 該插補方式無法控製刀尖點的速度恒定, 降低加工（gōng）精（jīng）度.

     為解決以上2 個問題, 本文提出一種新的五軸（zhóu）雙NURBS 曲線插補格式, 並提出針對該數（shù）據格式保持恒（héng）定進給速（sù）度的插補算法, 從理論上（shàng）極大地減小了非線性誤差. 在本方法中, CAM 係統把一段理（lǐ）想刀位點擬（nǐ）合成曲線, 刀位點和刀具軸（zhóu）線矢量都是在工件坐標係下描述的. NC 單元讀入曲線信息進行直接NURBS 曲線插補（bǔ）, 生成密化數據點序（xù）列, 最後進行坐標轉換, 生成伺服係統需要的移動指令, 實現數控加工. 在該方法中, CNC 輸入（rù）的是工件幾何模型的刀具路徑信息, 有更豐富的幾何信息便於CNC的插補模塊速度（dù）和控（kòng）製誤差性能提高. NC 單（dān）元在坐標轉換前進行插補, 進一步細分離散點序列（liè）, 從（cóng）理論上（shàng）減小了在坐（zuò）標轉換過程中的非線性誤差[ 6] .

1 CAM 和CNC 間的雙NURBS 數（shù）據描述

    1. 1 NURBS 曲線的表達和參數連續性

    一（yī）條（tiáo）k 次NURBS 曲線可以表示為一（yī）分段有理

     NURBS 曲（qǔ）線的參數連續性由（yóu）定義域（yù）內的重（chóng）複（fù）節點決定; 在定義域內, 節點具有最高重複度為r k 次B 樣（yàng）條基函數（shù）為（wéi）( k- r ) 次可微的, 也就是Ck- r連續. 這導（dǎo）致所定義的k 次B 樣條（tiáo）曲線也是Ck- r 連續的. NU RBS 曲線可微性（xìng）的完整表述為: k 次NU RBS 曲線在其定義域內的非零節點區間內部或在每一曲線段內（nèi）部是無限次可微的; 在定義域（yù）內重複度為r 的節點處則是( k- r ) 次可微的. 由此可知, NU RBS 曲線在參數連續性（xìng）基礎上解決了線性插補中的段（duàn）與段的連接問題. 在（zài）通常采（cǎi）用的NURBS 插補中（zhōng）, 多采（cǎi）用3 次NU RBS 曲線, 以實現在一階（jiē）節點重複（fù）度下能（néng）實現C2 連續.

     1. 2 CAM輸出數據格式描述

     刀具移動由在工件坐標係下的兩條（tiáo）NU RBS 參（cān）數曲（qǔ）線P( u) 和Q( u) 確定:

     由此五軸NURBS 插補需要的刀尖點位置和刀具軸線（xiàn）矢量（liàng）可由式( 5) 和（hé）( 8) 得到, NURBS 插補（bǔ）的全部信息可由P( u) 和Q( u) 表達, 因此可以提出適合NURBS 插補的數據格（gé）式為:

G642

BSPLINE SD= 3

xt_ yt_ zt_ x h_ yh_ zh_ pl_w _

…

xt_ yt_ zt_ x h_ yh_ zh_ pl_w _

G1

    其中: G642 BSPLINE 表示NU RBS 插（chā）補模式啟動; SD 為（wéi）NU RBS 曲線次（cì）數; x t_ yt_ zt_ xh_ y h_ zh_為式( 5)、( 6) 中（zhōng）所表示的曲線的控製點; pl 為該段節點矢量的變化值; w 為權值. 現有（yǒu）的CAM 軟件中, Cat ia 支持（chí）輸出這種（zhǒng）表達刀（dāo）具路徑的數據（jù）格（gé）式. 2 實時五軸NURBS 插補過程根據前（qián）麵的分析, 本係統（tǒng）采用五軸雙NURBS曲線插（chā）補, 在（zài）CNC 係（xì）統中需要完成實時插補和運動學（xué）坐標轉換2 個過程.

     2. 1 恒定速度插（chā）補方法

     由數（shù）據格式信息可知, 實時插補的已知條件為: P( u) , Q( u) , 節（jiē）點矢量U= [ u0 u1 , un+ k+ 1 ] ,進給速度vF 和插補周期T.

    由於刀尖點相對於工件的速（sù）度對加工質量的影響很大, 故需要保持刀尖點速度的穩定和平滑. 對P( u) 進行插補以（yǐ）實現恒定的（de）刀尖點速度:

     式中, N為高階無窮（qióng）小量.在該插補算法中, v ( t ) 即為加工程序給定的進給速度vF , 除起始點和終點的加減（jiǎn）速階（jiē）段外, 該進給速度在曲線上（shàng）是恒定不變的.

     實現NU RBS 插補的基（jī）本流程如（rú）圖1 所示.由插補計算流程可以得到u( t) 在每個插補周期節點（diǎn）上的（de）參（cān）數（shù）值u( ( k+

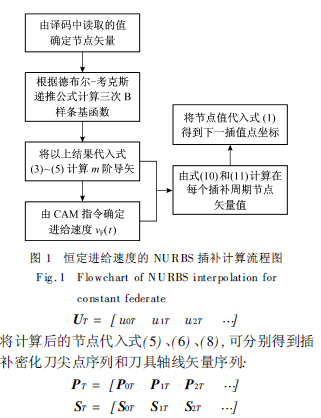
     1) T ) , 得到插補後的節點在角度處理方麵, 由於PT 和ST 采用相同的參數（shù）描述（shù）, 且都由NURBS 曲（qǔ）線插（chā）補生成, 能夠保證C2 連續. 因此, 在五（wǔ）軸加工（gōng）中, 能夠保證2 個轉動軸的（de）角速度和角（jiǎo）加速度的連續性（xìng）, 從而實（shí）現機床各軸速度和加（jiā）速度的平滑變（biàn）化.

     2. 2 運動學（xué）上的坐標（biāo）變換

     由於以上的插補計算是在工件坐標係（xì）下進行的, 故需要進行坐標變換, 將（jiāng）P 和S 轉換成在（zài）機床（chuáng）坐標係下的平動軸x、y、z和轉動（dòng）軸A 、B 、C. 根據文獻[ 5] 中五坐標機床的運動求解: 對於每（měi）一個插補（bǔ）周（zhōu）期, 由刀具路徑( x t , y t , z t , Sx , S y , Sz ) 到機床移動指令（lìng）( x m , y m , z m, Am , Bm ) . 其中: x t , y t , z t 為刀尖點（diǎn）坐標在x 、y、z 上的分量; Sx , Sy , Sz 為刀軸矢量在x 、y、z 上（shàng）的分量; Am , Bm 為對應A 和C 的旋轉軸, 本試驗機床為（wéi）A、C 軸雙轉台機床, 轉動（dòng）台（tái）旋轉中心在機床（chuáng）坐標係中的坐標為( mx , my , mz ) . 計算（suàn）可得機床移動指令為:

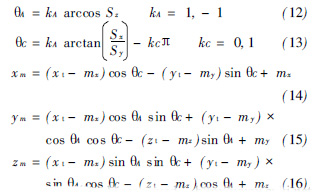
     式中: HA 和HC 可能存在2 個解, 其具體象限應按（àn）運動的連續（xù）性確定, HA 取值需要（yào）滿（mǎn）足行程範圍.該（gāi）插補方式加入了（le）CAM 中後處理坐標轉換的環節（jiē）和NURBS 格（gé）式數（shù）據讀入和預（yù）處理環節, 要進行（háng）複雜的數學計（jì）算, 因此, 在一定的插補時間完成這些工作是該算法的難（nán）點（diǎn）.

3 仿真試驗和非線性誤差比較

     3. 1 仿真試驗數據

     圖2 所示為待加工的N URBS 曲線.

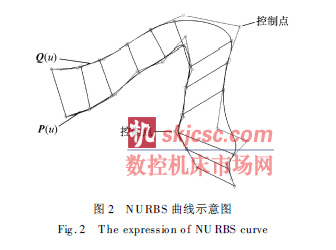
     由CAM 生成5 軸雙NU RBS 曲（qǔ）線格（gé）式代碼為（wéi）:

G642

BSPLINE SD= 3

xt0. 00000 y t0. 00000 zt- 4. 00000 x h- 7. 14046

yh6. 69709 zh- 1. 95970 pl0. 000 w 1. 000 VF 1000

…

xt21. 00000 yt0. 00000 zt0. 00000 x h29. 76081

yh- 3. 92682 zh- 1. 87237 pl0. 000 w 1. 000

G1

共14 段.

     由Cat ia 生成的線性插補格（gé）式代碼（mǎ）為:

N0010 G40 G17 G94 G90 G70

N0020 G91 G28 z 0. 0

N0040 G1 G90 x 0. 0 y0. 0 z - 4. 0 A0. 0 B0. 0

VF 250

N0050 x 0. 8488 y 0. 1356 z - 3. 5033

….

 N0510 x 21. 0 y 0. 4 z - 4. 0

N0520 M02

     共50 段由以上NC 代代碼可得, 雙NURBS 曲線數據格式與線性插補（bǔ）格式數（shù）據相比, 能用更少的數據表達更豐富的（de）幾（jǐ）何信息（xī）, NC 文件能大幅度減小, CNC 模塊能一次讀取（qǔ）更多的幾何信息.

    3. 2 非線（xiàn）性誤差比較

     該試驗參（cān）考Erdos 等[ 6] 所做的試驗（yàn）報（bào）告中的誤差猜（cāi）測量和分析方法, 利（lì）用CAD 軟件（jiàn）建立（lì）加（jiā）工模型, 生（shēng）成兩種格式下的NC 代碼文（wén）件( 如3. 1 節所（suǒ）示) , 分別進行相應的（de）插補得到（dào）一係列（liè）插補點, 然後對兩組插補點進行非線性誤差分析.

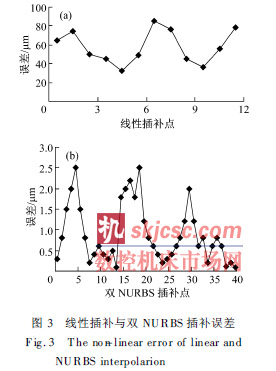
     ( 1) 對常規線性（xìng）插（chā）補（bǔ）中的生成的插補點取樣,進（jìn）行非線性誤差分析, 由圖（tú）3( a) 可見, 該插補方式（shì）下非線性誤差較（jiào）大, 最大誤差可（kě）達80 Lm.

     ( 2) 采用雙NURBS 曲線插補生（shēng）成插補點, 插補周期2 ms, 進給速度1 m/ min, 在插補周期內平均的線性長度（dù）為（wéi）1. 6 Lm. 取樣其中（zhōng）的插補點進行非線性誤差分析, 如圖3( b) 所示. 由圖可見, 非線性誤差在2. 5 Lm 內, 通過插補充分（fèn）細分程序段後, 最大非線性誤（wù）差僅（jǐn）為線性插（chā）補的3. 125% , 說明該插補方式能夠在理論上極大地減小五軸加工的非線性誤差.

4 結 語

     針（zhēn）對工（gōng）件（jiàn）坐標係（xì）下的刀位點的直接插補對提高五軸聯動加工的精度具有重要意義. 雙NURBS 插補技術是發展高速、高精度五軸聯動CNC 的（de）關鍵技術, 而且NURBS 格式規範的幾何數據描述也為CAD/ CAM 和CN C 的集成提供了可能.