摘要（yào）：機械臂軌跡規劃是機器人運動規劃領域中至關重要的經典研究方向（xiàng）之一。隨著機器人時代的到來，機械臂在工業製造中得到了廣泛的應用，如何更好的利用機械臂的運動性能，獲得運行時間較短或者消耗能量更少的運動軌跡成為人們關注的重點。
    
       關鍵詞：軌（guǐ）跡規劃，動為學模型（xíng），時（shí）間最優，能量最優

        引言
 
        在（zài）最大化化（huà）器人係統的生產效率方麵，時間最優運動規劃一直是一個很重要的課題。一壟常用的求解最短時間的軌跡規劃方法通常隻用到機器人（rén）的運動學模型，而沒有用（yòng）到機器人的動力學（xué）模型（xíng），這樣的規劃結果往往不能充分發揮機器人的潛力。
  
        結合第二章介紹的機械臂（bì）動為學模（mó）型（xíng）參數辨識方法，那麽可Ｗ辨識出機械臂的動力學模型，進而使用更（gèng）為有效的基於（yú）機械臂動力學模型的軌跡規劃方法（fǎ）。本章采用了Ｖｅｒｓｃｈｅｕｒｅ［５６：ｉ等人提（tí）出的基於凸優化求解時間最優軌跡規劃方法，並在此基礎上添加了表示能量和力矩變化率的代價函數，使得規劃軌（guǐ）跡更加易於機械臂的（de）執（zhí）行。
  
        本章的組織結構如下：３．２節介紹了基本基於力矩約束的時間最優軌跡規劃問題；３．３節闡述了如何將基本時間最優問題轉化到（dào）凸優化控製問題；３．４節對此凸優化（huà）控製（zhì）問題進行拓展（zhǎn），添加額外（wài）的目標函數和約束條件；３．５節介紹了此凸優化控製問題的數值解（jiě）法（fǎ）；３．６節Ｗ六自由度機（jī）械（xiè）臂為目標進行軌跡規劃，驗證此方法的有效性。
  
       ３．２基（jī）本問題描述（shù）
  
       ｉｖ自由度機械臂的動為學運動模型可Ｗ表示為如式（２．１）所示（shì）的關節力矩Ｔ（s） ＂關於各關節角ｇｅ巧＂的函（hán）數。事實上機械臂的（de）軌跡規劃問題一般都是建立（lì）在己知路徑上的，對於關節空間（jiān）中的路（lù）徑我們可Ｗ用t（ｓ）來表示，其（qí）中偽位移Ｓ是一維路爸坐標係。這個（gè）路徑坐標係是由機械臂末端在巧卡爾（ěr）空間中移動的路徑決定的，那麽軌跡的時間約束就可表示為坐標軸Ｓ和時間t的（de）關係（xì）式S（t)為了不失一般性，可レ乂假設軌跡起始於於t＝０，結（jié）束於t＝T並滿足s(0)＝０＜５(t)＜１＝s（t)，除此之外，由於（yú）現在考慮的（de）是（shì）時間最優軌跡（jì）規劃及其相關問題，故（gù）對於t包含（hán）（0，T），可化為Ｓ（t）的上（shàng）的毎一點都符合s（t）＞〇，並且在Ｓ（t）上的（de）絕大多數點上都符合s（t）＞０。同時（shí），對於給定的關節空間中的路徑ｇ（ｓ），關節的速度（dù）和（hé）加速度（dù）可（kě）Ｗ通過鏈式法則推導得到：

 
      
      
  
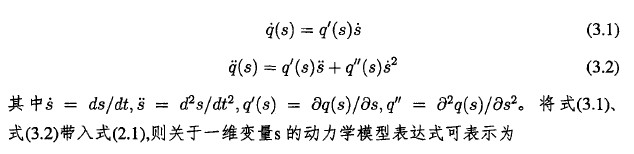
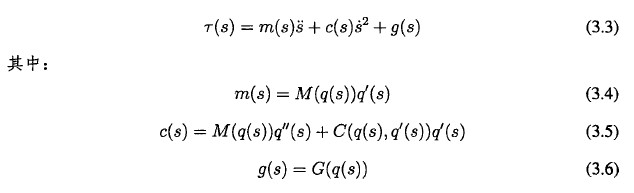
       那麽（me）基於為矩約（yuē）東的時間最優軌跡（jì）規劃可用數學表達式來（lái）據述：

      
  
      
       
  
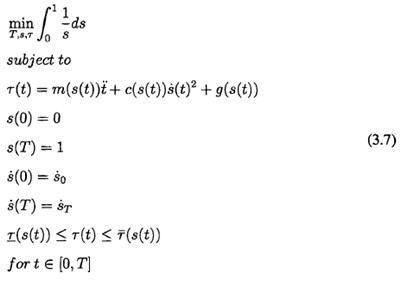
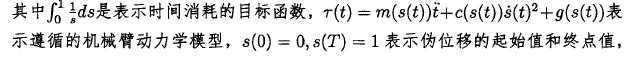
        基本時間（jiān）最優問（wèn）題到（dào）巧優化控製問（wèn）題的變（biàn）換
 
       對式口．７）這樣（yàng）形（xíng）式的非（fēi）線性約束下的目標函數，是無法直接看出所得到的局部最優解是否就（jiù）是全局最優解。而在ＳｈｍｅｒｆＷ這篇文章中，針對時間能量最優運（yùn）動規劃問題（tí）將式貨７）進行了特殊非線性變換，令其轉化為（wéi）一個受（shòu）非線性狀態控製約束，並包（bāo）含線性係統（tǒng）動為學模型、狀態微分和控製（zhì）輸入的最優控製（zhì）問題，同時證明了相對於控製輸入的漢密爾頓函（hán）數是曲函數，進而可（kě）レ乂證明擁有這種結構的問題的局部最（zuì）優解就是全局最優解，因此本文也對式（３．７）的一些（xiē）變量的進行非線性變換。
  
      首先，通過將原來得積分變量＾變換為５，此時目標函數變為
  
     
  
    
  
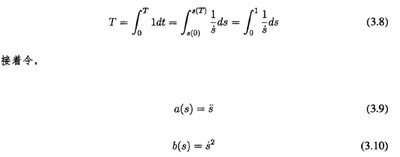
      因此式巧．７）描述的問題可１＾＾被重構為一（yī）個（gè）凸（tū）問（wèn）題
 
     
  
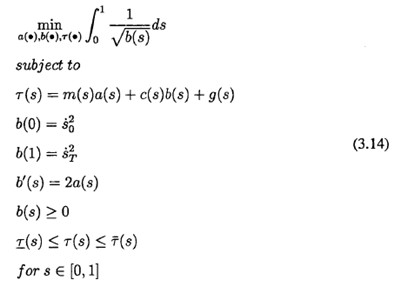
      式（３．１４）所描述的問題是田問題是因為所有（yǒu）的約束都是線性（xìng）的，而目標函數是凸函數。
  
      這個問題可Ｗ認為是代數微分形式的最優控製問題，它有著偽時間變量５，控製輸入ａ（ｓ），狀態微分６（３），代數形式的狀態ｒ（ｓ），線性係統的動態特性ｂ＇（ｓ）＝２ａ（ｓ）和與線性狀態相關的約東條件，Ｗ及初始狀（zhuàng）態和（hé）終止狀態的約束 條件。
  
     可以看到式（３．１４）僅僅隻有一個微分狀態，而代數形（xíng）式的（de）狀（zhuàng）態（tài）可通過Ｔ（ｓ）＝ｍ（ｓ）ａ（ｓ）＋ｃ（ｓ）６（ｓ）＋ｇ（ｓ）消除，並且表示時間的變量ｔ不再顯式的出現在方程中。這種問題重構形（xíng）式最大的價值在於：首先其目標函數和約（yuē）宋都轉變為了凸函數（shù），所求得的局部最優解即為全局（jú）最優解；其（qí）次，可Ｗ很容易的添加
目標函數和（hé）不等式約束，而（ér）不改變整個最優化控製問題的（de）凸性，這將在下麵的（de）章節（jiē）中進行討論；最後，利用數值方法可Ｗ非常有效的對（duì）這種表巧形式進行求解。
 
     ３．４擴展的西優化控（kòng）製問題
  
     在３．４．１節中介紹一些實用的約束條件（jiàn），在３．４．２節中本文提出了額外的目標（biāo）函數，這些目標函數的增加是（shì）為了使（shǐ）得規劃出來的軌跡為矩變化較小，更加易於實（shí）際機械臂的執行，最後在３．４．３節（jiē）中將這些目標函數和約宋結合起來，得到一個更加一（yī）般但仍能保持凸（tū）特性的最優化控製（zhì）問題。
 
 
      ３．４．１其他不等式約束
  
      除了各（gè）關節為矩約束，還有其他一些很有用的約束。
  
     １．速度約束（shù）：一些特別的任務中可能要（yào）求加入（rù）速度限製，此時（shí）可Ｗ在（zài）第ｉ個關節上施加對稱的最小速度約束－和最大速度約束亮（５），其具（jù）體表達式如下所示：


   
 
  
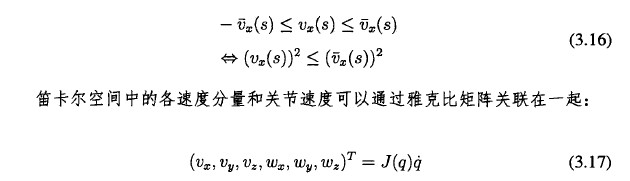
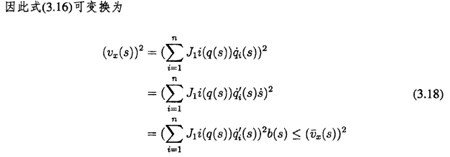
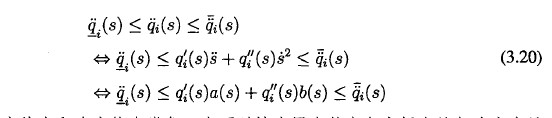
     加速度約束和速度約（yuē）束類似，化可ｗ被應用在笛卡（kǎ）爾空（kōng）間中的加速度分量（liàng）上，而不管是作用在（zài）關節空間（jiān）中的加速度約宋還是作（zuò）用在笛卡爾空間中的加速度約束都可Ｗ被寫成一個統一的形式：
  
    
 
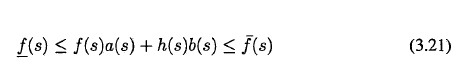
     ３．４．２目標函（hán）數優化
 
     由於時間（jiān）最優軌跡通常有著ｂａｎｇ－ｂａｎｇ特性，並不易於機械臂的執行。所Ｗ本文在這個基於凸優化的問題框架中添加一些其它目標函（hán）數，從而得到一條更加理想的、考慮其它（tā）準則的時間最優運動軌跡。
  
     １．能量消耗：
 
     第關（guān）節力矩的平方（fāng）關於時間的積分可Ｗ表示為：
 
    
  
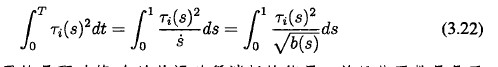
     這（zhè）個目標函數表示的是驅動第ｉ個關節運動所消耗的能量，並且此函（hán）數是凸函數。
   
     ２．為矩變化率絕對值（zhí）的（de）積分：
  
    
  
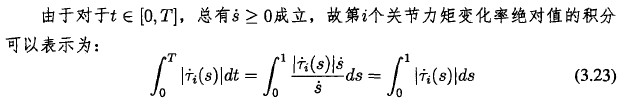
     因為Ｎ是（shì）關於Ｅ的巧函數，所Ｗ式（３．２巧表示的目標函數也（yě）是凸函數。雖然這樣的目標函數並（bìng）沒有比（bǐ）較直觀的物理解釋，但是在最終的目標函數（shù）中（zhōng）包含這項可Ｗ減小關節為矩的變化率。
  
     ３．４．３廣義的（de）時間最優問（wèn）題
  
     結合式口．７），式（３．２２）和式口．２３）所表示（shì）的目標函數與式（３．７），式口．１９）和式口．２１）所表示的（de）巧宋項，可Ｗ得到一個廣（guǎng）義的廣義最優控製問題
  
    
  
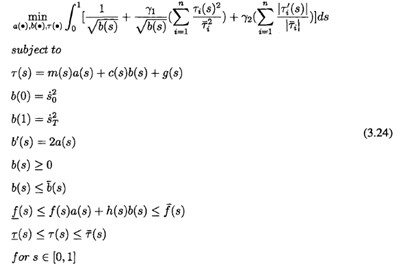
     由於這個表適式中的（de）目標函數和（hé）不（bú）等式約束都是凸的，而等式約束是線性的，所上述廣義時間最優問題還是凸的。
  
     ３．５數（shù）值計算（suàn）
 

  
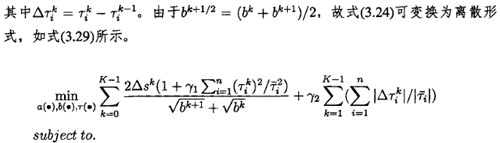
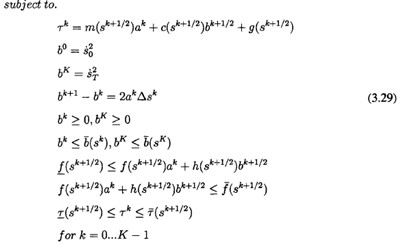
     由於式（３．２９）描述的問題為凸，所Ｌ乂任何局部最優解也是全局最優的（de）。因此可Ｗ任（rèn）意選取（qǔ）一個非線性求解器來求解這個問題。本文采用的是ｍａｔｌ油中的ＹＡＬＭＩＰ王具箱進行求解，這是一種可Ｗ求（qiú）解高級優（yōu）化問題工具箱，並且有多種求解器可供（gòng）選（xuǎn）擇。一旦求解出變量護的值（zhí），則可通過束解＊（ｓ）得到表示路徑（jìng）坐標軸（zhóu）和時間的關係式Ｓ的，而＊（ｓ）的表達式如下所示：
  
     
  
     ３．６實驗與分析
  
     本節（jiē）在ＡＢＢ六軸工業機器人ＩＲＢ１２０上（如困３．４所示）實現基於凸優化的時間最優軌跡規劃，３．６．１節介紹了實（shí）驗任務和目標路徑，３．６．２節說明了實驗結果。
  
    
  
     ３．６．１實驗（yàn）任務說（shuō）明
   
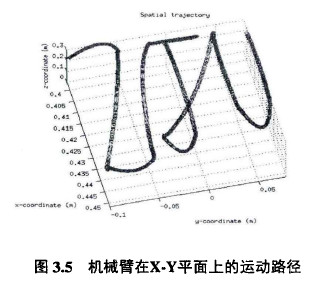
     本實驗是用ＩＲＢ１２０六（liù）軸工業機械臂（bì）執行複雜的書寫任務，書寫任務為在水平麵上寫出＂ＺＪＵ＂字樣（如圖３．５所示），書寫要求是盡可能快的完成這一任務。
  
     
  
     為了實現（xiàn）基於動力學模型的最優（yōu）時間軌跡規（guī）劃，需要知道ＩＲＢ１２０六軸工業機（jī）械臂的動（dòng）為學模型參數，由於本實驗室的ＩＲＢ１２０機（jī）械臂缺芝參數辨識的條件（這在上一章有所介紹），故此處軌跡規（guī）劃使用的機械臂動力學模型參數是由ＡＢＢ麽司提供的。
 
     ３．６．２實（shí）驗結果
  
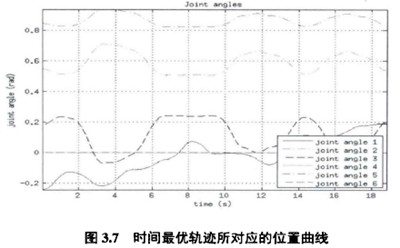
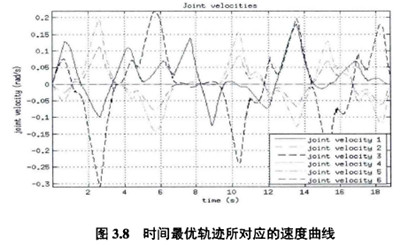
     根據３．５小節提出的數值計算方法（fǎ），可得到完成書寫’’ＺＪＵ＂任務的最短時間為６．４巧。如（rú）圖３．６所示的是完成這一任務的機械臂六個自由度關節的驅動力矩曲線，可看到在任意一個（gè）時刻都有一個關節的（de）驅動為矩是處於滿負荷運行的（de），由於第一關節總是（shì）承受這絕（jué）大部（bù）分的重力作用，所Ｗ其很多時間都是處於（yú）最大力矩控製狀態是可Ｗ理解的。圖３．８表示的是時間最優軌跡規劃對應的位置和速度曲線，由速度曲線（xiàn）可レ乂看出規劃軌（guǐ）跡速度在很多地方都有尖角，這也符合控製為矩的突變。
  
     
  
    
  
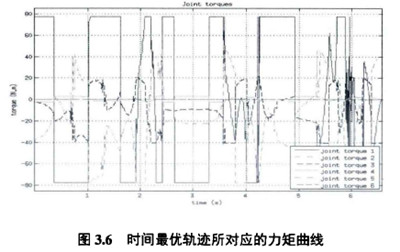
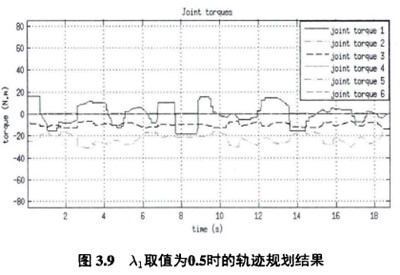
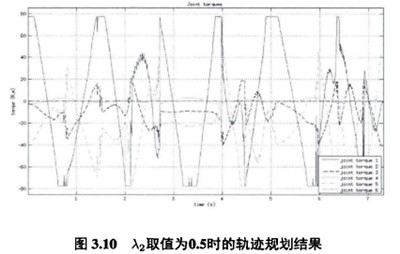
     可見單純的時間最優軌跡規劃力矩變化（huà）十分劇烈，這種軌跡的執行會（huì）造成機械臂很大的負擔，並且在實際的機（jī）械臂（bì）上也（yě）是很難實現的，本章在凸優化框架基礎上加入的代表能量消耗的目標函數和代表為矩變化率的目標函（hán）數就是為了解決這（zhè）一問題。圖３．９表示的是考慮運動時間和能量消耗時的軌跡規劃結果，可Ｗ看到運動的時間增大到１８．３ｓ而運動過程中各關節最大輸出為矩顯著減小（xiǎo），同時根據式（shì）（３．２４）可Ｗ通（tōng）過增大Ａｉ的取值使得規（guī）劃出的軌跡的能量消耗變小。圖３．１０表（biǎo）示的是考慮運動時（shí）間（jiān）和為矩變化率的軌跡規劃結果（guǒ），可Ｗ看到（dào）運動的時間增大到７．２ｓ而（ér）各關（guān）節力矩變化率降低了，同時根（gēn）據式（３．２４）可Ｗ通過增大乂２的取值使得規劃（huá）出的軌跡的力矩變化率進一步減小。
  
    
  
     
  
     由於六自由度機械臂ＩＲＢ１２０並沒有提供力矩輸入（rù）的接口，本次實驗規劃出來（lái）的軌跡沒（méi）有在實際機械臂上運行，然而軌跡規劃的運（yùn）動軌跡符合機械臂動為學橫型等（děng）一係（xì）列約束條件，故可認為規劃結果在實際（jì）機械臂上化是（shì）可行的。
  
    
  
     ３、 本章小結
  
     本章（zhāng）介紹了用凸優化方法求解時間最優軌跡規劃問題，拓展了優化的目標函數，考（kǎo）慮（lǜ）能量消耗和各關節為矩的變化率，使得得到的（de）軌跡更加平滑，易於機械臂（bì）的實現。最後針對六自由度機械臂ＩＲＢ１２０進行了最優軌跡的規（guī）劃（huá），驗證了算（suàn）法的（de）有（yǒu）效（xiào）性。