１　單對齒輪的齧合剛度模型

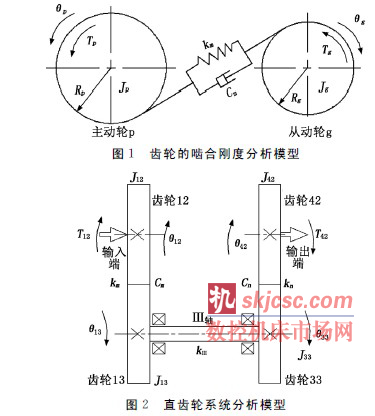
      本（běn）文主要考慮在輸入轉速和（hé）負載扭矩不變的條件下，輸出齒輪轉角的變化情況。齧合剛度模型（xíng）是一個最基本的齒輪副分析模型，隻（zhī）考慮了齒輪副本身的影響因素（sù），忽略了傳動軸的彎（wān）曲變形、扭（niǔ）轉變形和軸承的支撐剛度等。齒輪的齧合剛度（dù）分析模型如圖１所示。

      其中，θｐ、θｇ分別為驅動齒輪、從（cóng）動齒輪的扭轉位移；

      Ｒｐ、Ｒｇ分別為驅動齒輪（lún）、從動齒輪的基圓半徑；Ｔｇ、Ｔｐ分別為負載轉矩和輸（shū）入轉矩；Ｊｐ、Ｊｇ分別為驅動齒輪、從（cóng）動齒輪（lún）的（de）轉動慣（guàn）量；ｋｍ為輪齒的齧合綜合剛度（dù）；ｃｍ為輪齒的齧合阻尼。

      齒輪齧合剛度模型的建模條件是：驅動輪ｐ勻速轉動，負載扭矩Ｔｇ為（wéi）恒定負（fù）載。假設在齧合線方向上齒輪的相對位移為ｘ，則ｘ＝Ｒｐθｐ－Ｒｇθｇ。由於齒輪間的齧合力Ｆｋｍ＝ｃｍｘ　·＋ｋｍｘ，則Ｆｋｍ為：

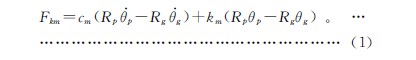
      齒輪副的動力學方程為：

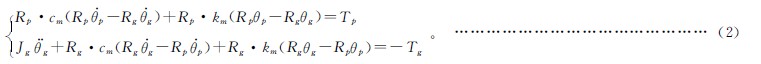
      ２　傳動鏈齧合（hé）剛（gāng）度動力學模型

      ２．１　直（zhí）齒輪係統齧合剛度動力學模型（xíng）［１］

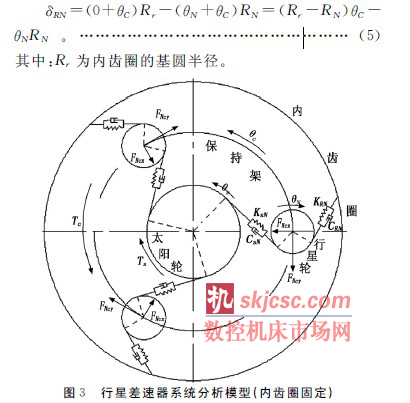
      在單對齒（chǐ）輪副齧合（hé）剛（gāng）度分析模型的基礎之上，考慮了傳動軸的（de）扭轉剛度（dù）之後就形成了（le）直齒輪子係統（tǒng）的（de）動力學模型，如圖２所示。其中，Ｊ１２、Ｊ１３、Ｊ３３、Ｊ４２分別為各直齒輪的轉動慣量；θ１２、θ１３、θ３３、θ４２分別為各直齒輪的（de）旋轉角；Ｔ１２為輸入端的驅動扭矩；Ｔ４２為輸出端的負載扭（niǔ）矩；ｃｎ為齒輪（lún）副的齧合（hé）阻尼；ｋｎ為齒輪副的齧合剛度；ｋⅢ為（wéi）Ⅲ軸（zhóu）的扭轉剛度。

      直齒輪係統分析模型的前提條（tiáo）件（jiàn）是：輸入齒輪為（wéi）勻速旋轉運動（dòng），輸出負載扭矩為恒（héng）定負載（zǎi）。結合式（２）和（hé）牛頓力學理論，可以得到如下的微（wēi）分方程組：

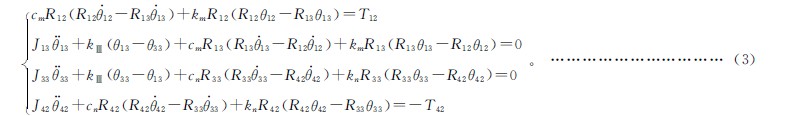
      其中：Ｒ１２、Ｒ１３、Ｒ３３、Ｒ４２分（fèn）別為各直齒輪（lún）的基圓半徑。

      根據Ｌａｐｌａｃｅ變換（huàn）對式（３）進行處（chù）理，得到關（guān）於變量ｓ的多元一（yī）次方程組，代入設（shè）計（jì）數（shù）據（數據保密），得出直齒輪子係統（tǒng）動力學（xué）模型的（de）轉角傳遞函（hán）數Ｇ４２為：

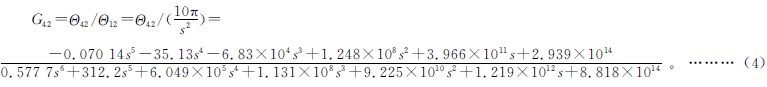
      其中：θ１２、θ４２分（fèn）別是θ１２、θ４２的Ｌａｐｌａｃｅ變換。

      其中：ＲＳ、ＲＮ分別為太陽輪和行星輪的基圓半徑。

      （２）內齒圈與行星輪在齧合線方向上的相（xiàng）對位移δＲＮ為：

       ２．２．２　齒（chǐ）輪齧合力的（de）計（jì）算

      （１）內齒圈與行星輪的齧合力ＦＲＮ為：

      將式（４）～式（８）代入到式（９）、式（shì）（１０）中，並轉化成方程組的形式為：

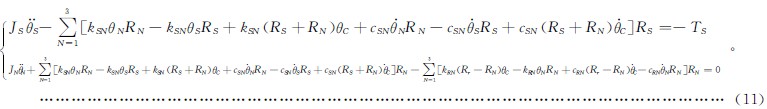
      式（１１）中的變量為：ＴＣ，θＳ，θ１，θ２，θ３。由於（yú）θ１＝θ２＝θ３，故用θＮ來替代，使之滿足θＮ＝θ１＝θ２＝θ３。將
 

      式（１１）進行Ｌａｐｌａｃｅ變（biàn）換，代入設計（jì）數據（數據保密）求（qiú）得轉角傳遞函數ＧＣＳ：

      其中：θＣ、θＳ分別為θＣ、θＳ的Ｌａｐｌａｃｅ變換形式。

     ３　傳動鏈動力學總模型

      將前（qián）麵的（de）直齒輪係統和行星差（chà）速器係統的動力學模型進行綜合（hé），用轉角傳遞函數來（lái）表示最終的動力學模型。由於這兩個子係統是串聯關係（xì），因（yīn）此（cǐ）總傳動鏈模型的轉角傳遞函數為：

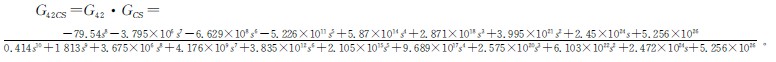
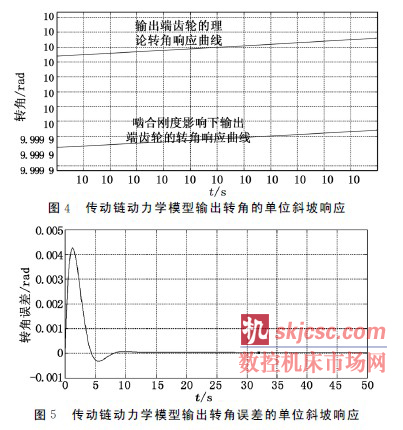
      運（yùn）用ＭＡＴＬＡＢ軟件對轉角傳遞函數進行單位（wèi）斜坡響應分析，得到的曲線如圖４、圖５所示。

      ４　結論

      由圖４、圖５可得（dé）出如下結論：①在齧合剛度影響下的傳動鏈轉角的輸出曲線與（yǔ）輸入曲線之間存在著轉角誤差，這會影（yǐng）響該機床傳動鏈的傳動精（jīng）度和傳遞的準確性；②轉（zhuǎn）角誤差響應曲（qǔ）線經過一定的震蕩後期後（hòu），穩定為一條（tiáo）水（shuǐ）平（píng）的直線，這表明齧合剛度影響下的傳動鏈轉角誤差是一個不隨時間變化的恒定；③齒輪的理論轉角相應曲線的斜率與齧合剛度模型下的轉（zhuǎn）角響應曲（qǔ）線斜率基本相同，說明（míng）齧合剛（gāng）度對傳動鏈的（de）傳動比基本沒有影響。